Chip Award Winner
Product of the Year 2012
IMU Brick¶
Features¶
- Full fledged AHRS with 9 degrees of freedom
- No accumulating errors, no gimbal lock!
- Factory calibrated, easy to recalibrate
- Calculates quaternions as well as roll, pitch and yaw
- One USB port and two Bricklet ports
Description¶
The IMU Brick is equipped with a 32-bit ARM microcontroller and an inertial measurement unit. It has 9 degrees of freedom and consists of a 3-axis accelerometer, magnetometer and gyroscope. The board computes quaternions as well as roll, pitch and yaw information, it is a complete attitude and heading reference system. The API allows access to the calculated data and also the acceleration, magnetic field and angular velocity for the three axes. If the quaternion representation is used, the IMU Brick does not have a gimbal lock, as known from Euler angles.
It is compatible to other Tinkerforge Bricks and can be used within a stack. Two Bricklet ports can be used to extend the features of this device.
Controlling the device is possible in several ways. You can control it via a PC connection. This connection can be established directly with a USB cable or by other cable based (RS485, Ethernet) or wireless (WIFI) connections via an additional Master Brick with corresponding Master Extension (High Level Concept).
Since the firmware is open source it is possible to program the device directly (On Device Programming). Currently we are not offering an On Device API.
Technical Specifications¶
| Property | Value |
|---|---|
| Microcontroller | ATSAM3S2B (128kB Flash, 32kB RAM) |
| Current Consumption | 53mA |
| Acceleration, Magnetic, Angular Velocity Resolution | 12bit, 16bit, 16bit |
| Roll, Pitch, Yaw Resolution | 0.01° steps |
| Quaternion Resolution | 32bit |
| Bricklet Ports | 2 |
| Dimensions (W x D x H) | 40 x 40 x 16mm (1.57 x 1.57 x 0.63”) |
| Weight | 12g |
Resources¶
Connectivity¶
The following picture depicts the different connection possibilities of the IMU Brick.
Test your IMU Brick¶
To test the IMU Brick you need to have the Brick Daemon and the Brick Viewer installed (for installation guides click here and here) and the Brick Viewer has to be connected to the Brick Daemon.
Now connect the Brick to the PC over USB, you should see a new tab named “IMU Brick” in the Brick Viewer after a moment. Select this tab.
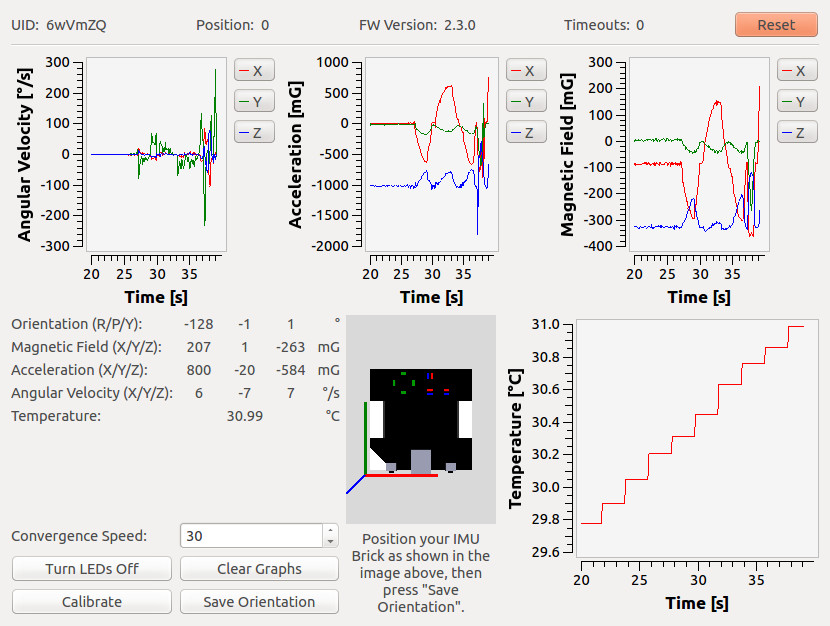
You can see all of the available data form the IMU Brick. If you hold the IMU Brick in the orientation as shown in the image and press “Save Orientation”, the movements that you make with the IMU Brick should be mirrored in the Brick Viewer. Before you press “Save Orientation” you should hold the IMU Brick still for about 15 seconds, so it can converge to the correct position.
After this test you can go on with writing your own application. See the Programming Interface section for the API of the IMU Brick and examples in different programming languages.
IMU Calibration¶
The IMU Brick comes factory calibrated and should work out of the box. It is however easy to recalibrate, if necessary.
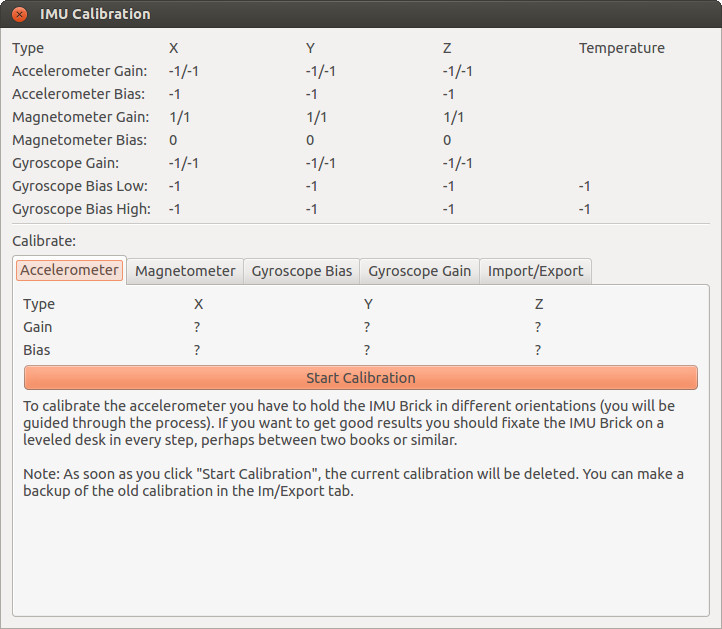
The factory calibration has taken place in a room without any significant interfering magnetic fields. If you want to operate the IMU Brick near something that has a magnetic field (e.g. near a motor), you will have to recalibrate the magnetometer in the exact position where it will be used later on!
To calibrate the magnetometer press on “Calibrate” in the Brick Viewer and choose the “Magnetometer” tab of the new window. Press “Start Calibration” and now change the orientation of the IMU Brick until the bias and gain values shown in the GUI do not change anymore. Press “Ready” when this is the case and you are done.
Accelerometer and gyroscope can be calibrated similarly, follow the instructions as given by the calibration tool. We recommend that you export the calibration before you start recalibrating the accelerometer and the gyroscope, so you are able to go back to the old calibration.
We recommend that you don’t try to recalibrate the gyroscope gain, it is not possible without suitable external machinery.
The factory calibration for your IMU Brick can be found at:
http://download.tinkerforge.com/imu_calibration/YOUR_IMU_UID.txt
Replace YOUR_IMU_UID by the UID of your IMU Brick. If you accidentally miscalibrated a sensor or you flashed a new firmware version, you can reimport the factory calibration. To do so go to the “IMU Brick” in the Brick Viewer, click the “Calibrate” button and select the “Im/Export” tab. Finally copy and paste the content of YOUR_IMU_UID.txt to the textbox and click “Import”.
Since Brick Viewer version 1.1.13 you can also click the “Restore Factory Calibration” button, that automatically downloads and imports the factory calibration for you.
Quaternions vs Euler Angles¶
We highly recommend that you use quaternions in your project rather than Euler angles (yaw, pitch and roll), since the latter exhibits a gimbal lock.
A formula to transform quaternions to rotation matrices can be found in the API documentation. Note that Euler angles always have an order in which they are applied. The order for the IMU Brick is: roll, yaw, pitch.
Computation of independent Angles¶
It is not possible to get angles for all 3 axis that are completely independent. At least at the gimbal lock positions there will be jumps of 180° for some of the angles. This is simply not possible otherwise.
If you want rotation angles for the x, y and z axis for a given base position, you have to rotate the quaternion according to your base position and calculate the angles after that. The following Python example does exactly that and it should be easy to understand and translate in other languages. Note that there are gimbal locks at +90° and -90° from each of the angles. The base position will be (0,0,0):
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from tinkerforge.ip_connection import IPConnection
from tinkerforge.brick_imu import IMU
import math
import time
class Q:
HOST = "localhost"
PORT = 4223
UID = "9yEBJVEHaem" # Change to your UID
def __init__(self):
self.base_x = 0.0
self.base_y = 0.0
self.base_z = 0.0
self.base_w = 0.0
self.ipcon = IPConnection() # Create IPconnection
self.imu = IMU(self.UID, self.ipcon) # Create device object
self.ipcon.connect(self.HOST, self.PORT) # Connect to brickd
# Wait for IMU to settle
print 'Set IMU to base position and wait for 10 seconds'
print 'Base position will be 0 for all angles'
time.sleep(10)
q = self.imu.get_quaternion()
self.set_base_coordinates(q.x, q.y, q.z, q.w)
# Set period for quaternion callback to 10ms
self.imu.set_quaternion_period(10)
# Register quaternion callback
self.imu.register_callback(self.imu.CALLBACK_QUATERNION, self.quaternion_cb)
def quaternion_cb(self, x, y, z, w):
# Use conjugate of quaternion to rotate coordinates according to base system
x, y, z, w = self.make_relative_coordinates(-x, -y, -z, w)
x_angle = int(math.atan2(2.0*(y*z - w*x), 1.0 - 2.0*(x*x + y*y))*180/math.pi)
y_angle = int(math.atan2(2.0*(x*z + w*y), 1.0 - 2.0*(x*x + y*y))*180/math.pi)
z_angle = int(math.atan2(2.0*(x*y + w*z), 1.0 - 2.0*(x*x + z*z))*180/math.pi)
print 'x: {0}, y: {1}, z: {2}'.format(x_angle, y_angle, z_angle)
def set_base_coordinates(self, x, y, z, w):
self.base_x = x
self.base_y = y
self.base_z = z
self.base_w = w
def make_relative_coordinates(self, x, y, z, w):
# Multiply base quaternion with current quaternion
return (
w * self.base_x + x * self.base_w + y * self.base_z - z * self.base_y,
w * self.base_y - x * self.base_z + y * self.base_w + z * self.base_x,
w * self.base_z + x * self.base_y - y * self.base_x + z * self.base_w,
w * self.base_w - x * self.base_x - y * self.base_y - z * self.base_z
)
if __name__ == "__main__":
q = Q()
raw_input('Press key to exit\n') # Use input() in Python 3
q.ipcon.disconnect()
How it works¶
With the sensor data gathered by the IMU Brick (angular velocity, acceleration and magnetic field), it is possible to apply sensor fusion to acquire an absolute orientation.
For this process often a Kalman Filter is used. The filter that is used in the IMU Brick is based on this paper by S. O. Madgwick. In our tests this new state of the art filter could achieve significantly better results than a Kalman Filter. Madgwick describes the approach of his filter as follows:
[...] the filter calculates the orientation by numerically integrating the estimated orientation rate. It is computed as the rate of change of orientation measured by the gyroscopes. The magnitude of the gyroscope measurement error is removed in the direction of the estimated error, which is computed from accelerometer and magnetometer measurements.
The following image shows the different steps of the filter:
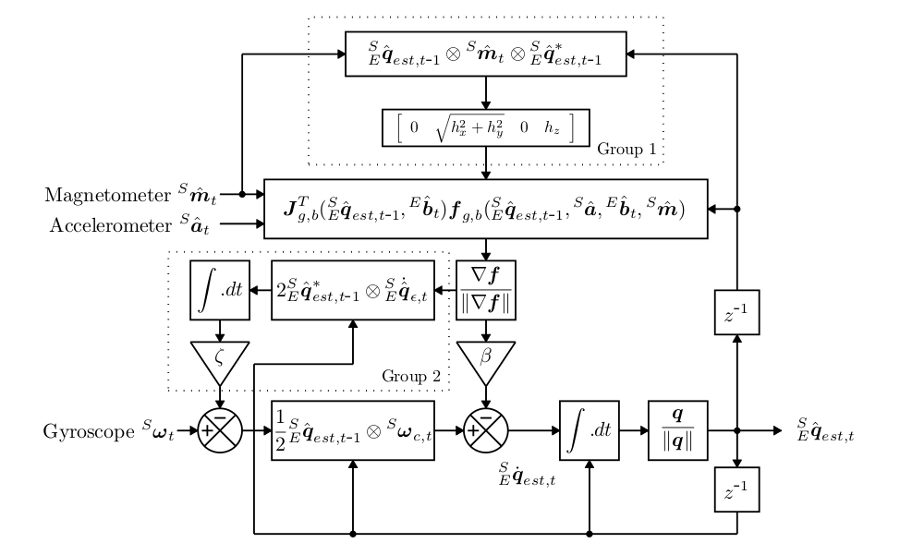
Image and explanation from S. O. Madgwick: “An efficient orientation filter for inertial and inertial/magnetic sensor arrays”, University of Bristol, April 2010.
Programming Interfaces¶
High Level Programming Interface¶
See High Level Programming Interface for a detailed description.
| Language | API | Examples | Installation |
|---|---|---|---|
| Modbus | API | ||
| TCP/IP | API | ||
| C/C++ | API | Examples | Installation |
| C# | API | Examples | Installation |
| Delphi | API | Examples | Installation |
| Java | API | Examples | Installation |
| PHP | API | Examples | Installation |
| Python | API | Examples | Installation |
| Ruby | API | Examples | Installation |
| VB.NET | API | Examples | Installation |
On Device Programming Interface¶
Note
Coming soon!
An API and documentation for direct on device programming (comparable to Arduino) is planned. You can however already use our firmware as a starting point for your own modifications (C knowledge required).
The content of this page is licensed under
Creative Commons Attribution 3.0 Unported License.
Follow us
